Cascades Towards Noise-Induced Transitions on Networks Revealed Using Information Flows
This paper examines noise-induced transitions in complex networks, identifying two key node roles: initiators, which propagate short-lived fluctuations to destabilize the system, and stabilizers, which encode long-term memory to restore stability. Using information-theoretic metrics, the study reveals a “domino effect” where noise cascades from low-degree to high-degree nodes, driving metastable transitions and tipping points. Our findings provide a framework for predicting and controlling critical transitions in systems like neural networks, ecosystems, and social dynamics.
WHEN NETWORKS FALL LIKE DOMINOES:
AN ESSENTIAL INTERACTION BETWEEN SHORT-LIVED AND LONG LIVED CORRELATIONS
— Cover of Journal Entropy featured our recent publication as a cover for the Special Issue 180th Anniversary of Ludwig Boltzmann
Authored by:
Casper van Elteren
Rick Quax
Peter Sloot
Share on X
Share on Bluesky
Research Highlights
Integrated mutual information reveals how short-lived fluctuations destabilize the system, while asymptotic information captures long-term memory that stabilizes new attractor states.
The domino effect is evident: low-degree nodes initiate destabilization by propagating noise, while high-degree nodes stabilize the system near tipping points. This transition in information flows provides predictive insights into critical transitions.
Initiators propagate noise and destabilize the system, while stabilizers encode long-term memory and stabilize metastable states. These roles can be manipulated to control systemic transitions.
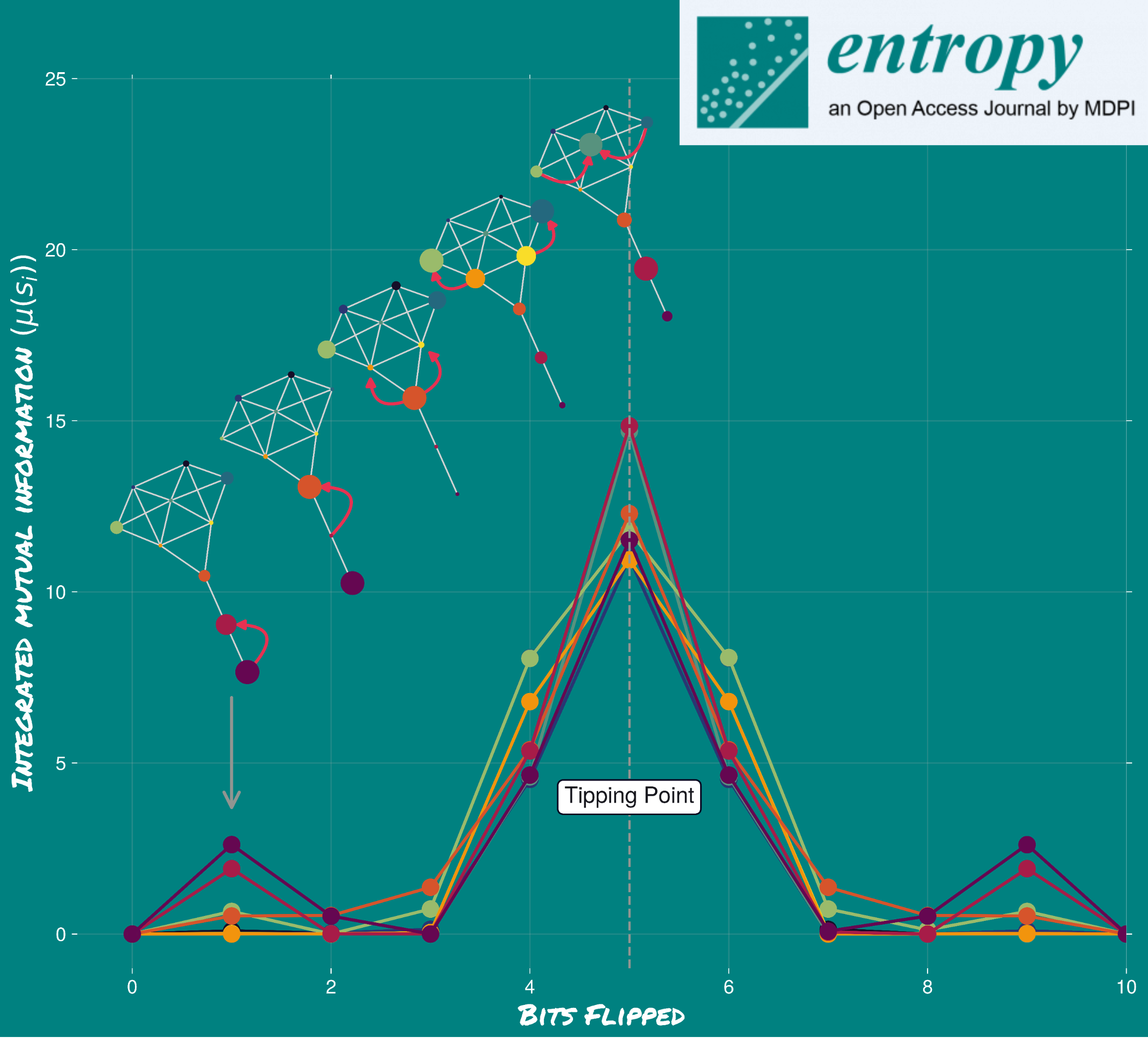
Trajectories Towards Tipping Points and Their Predictive power
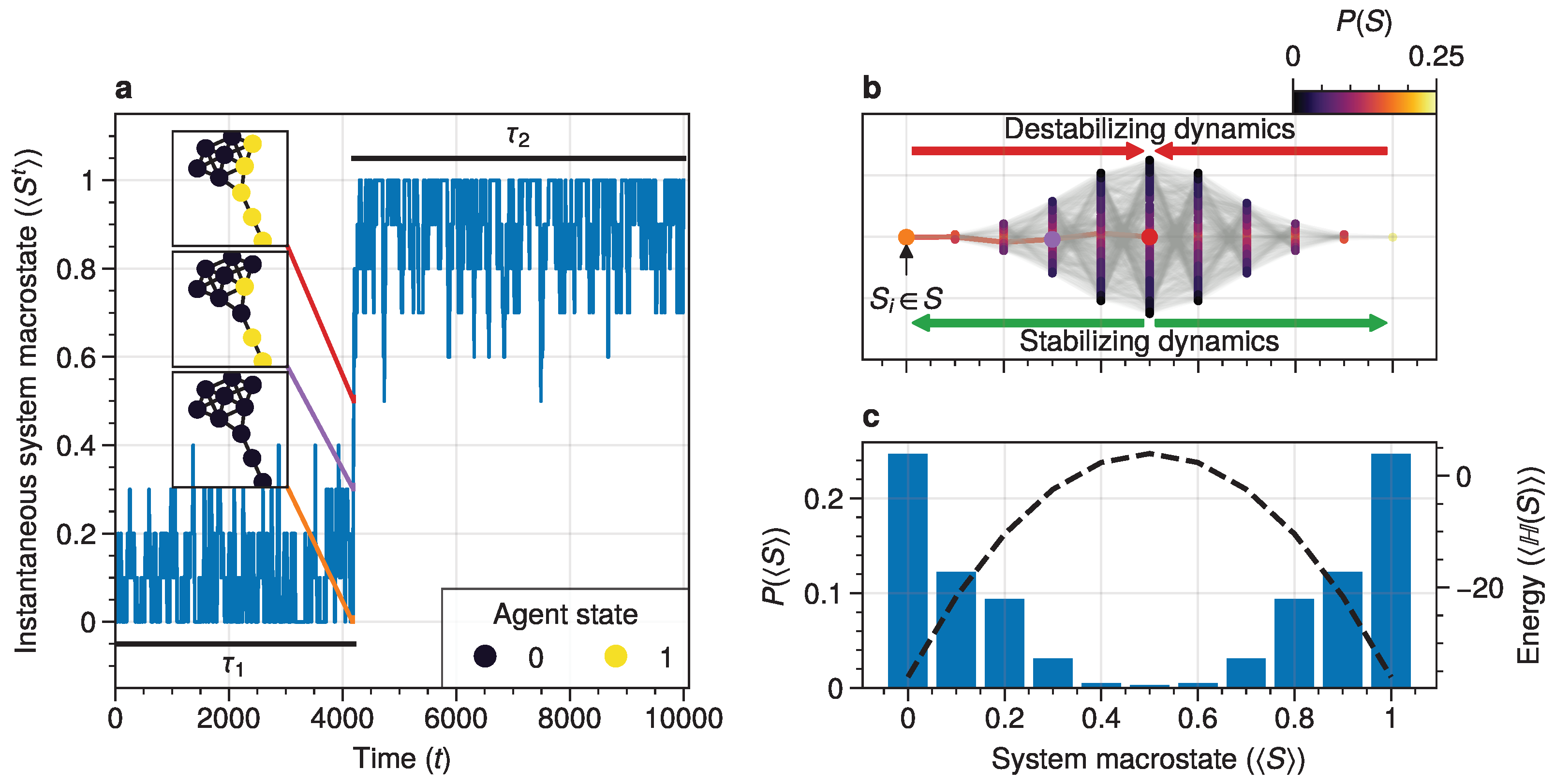
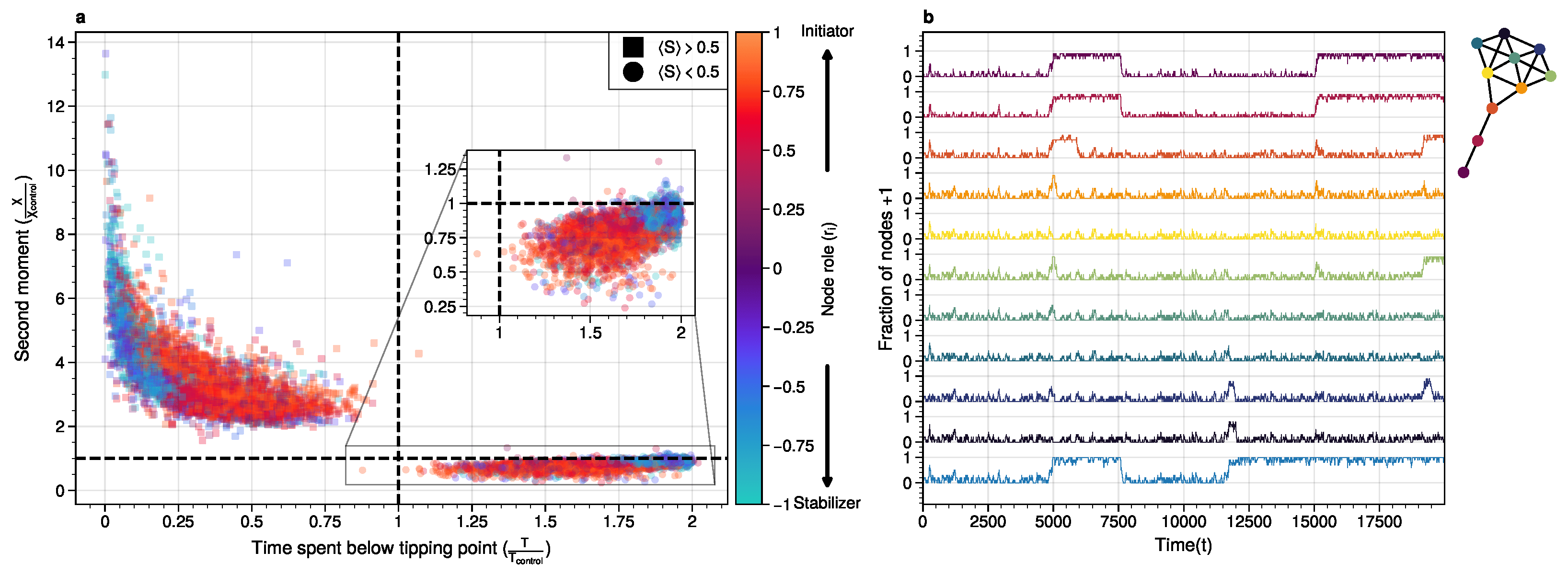
The cascade mechanism underpins metastable transitions, with low-degree nodes acting as initiators that trigger systemic change.
High-degree nodes provide stability by aligning with macrostates, while low-degree nodes drive transitions through noise propagation. Network structure plays a critical role in determining transition dynamics.
General Conclusions
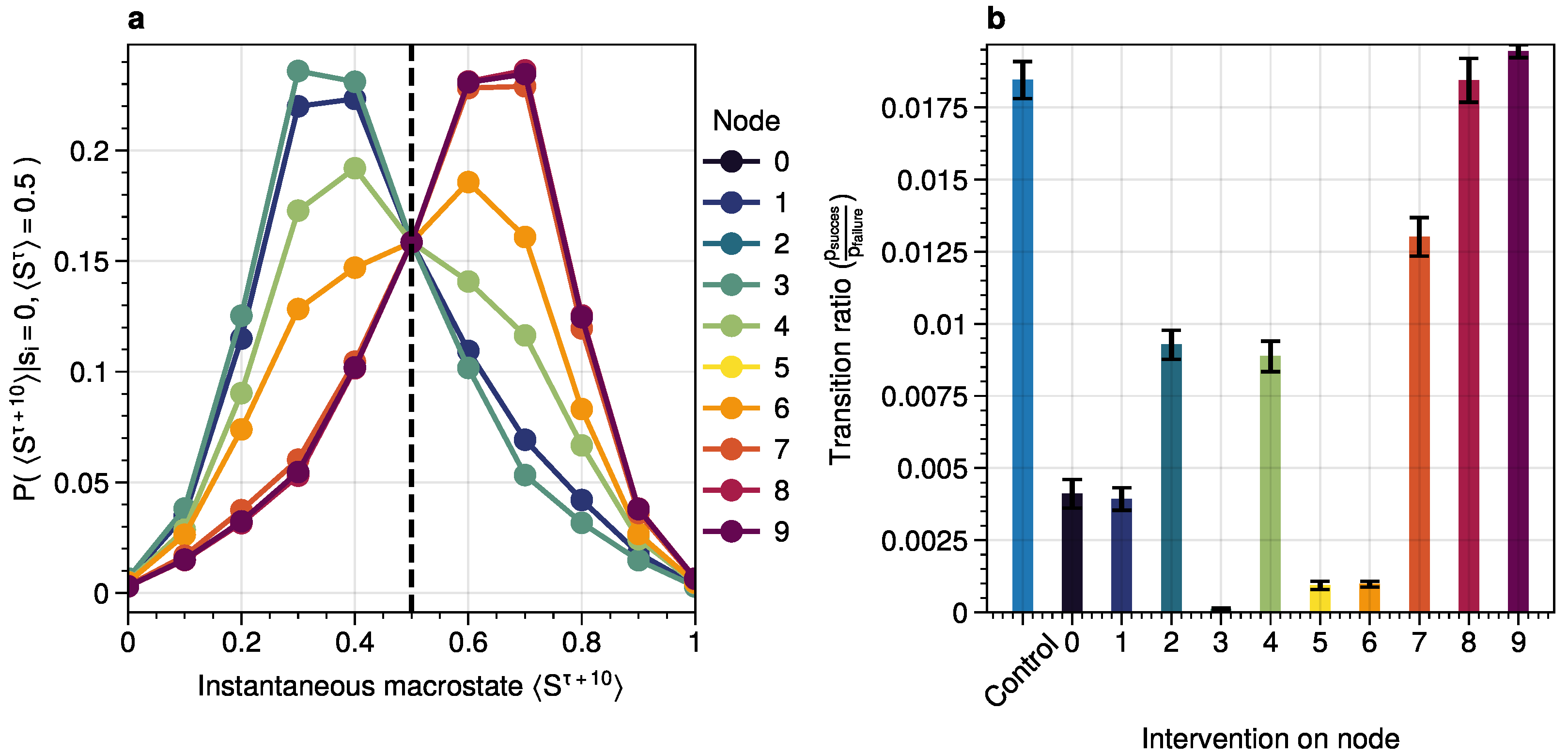
1. Role Differentiation: The study identifies two critical node roles—initiators and stabilizers—within dynamical networks:
-
Initiators propagate short-lived fluctuations that destabilize the system and push it toward a tipping point.
-
Stabilizers encode long-term memory that reverses destabilization effects and stabilizes new attractor states.
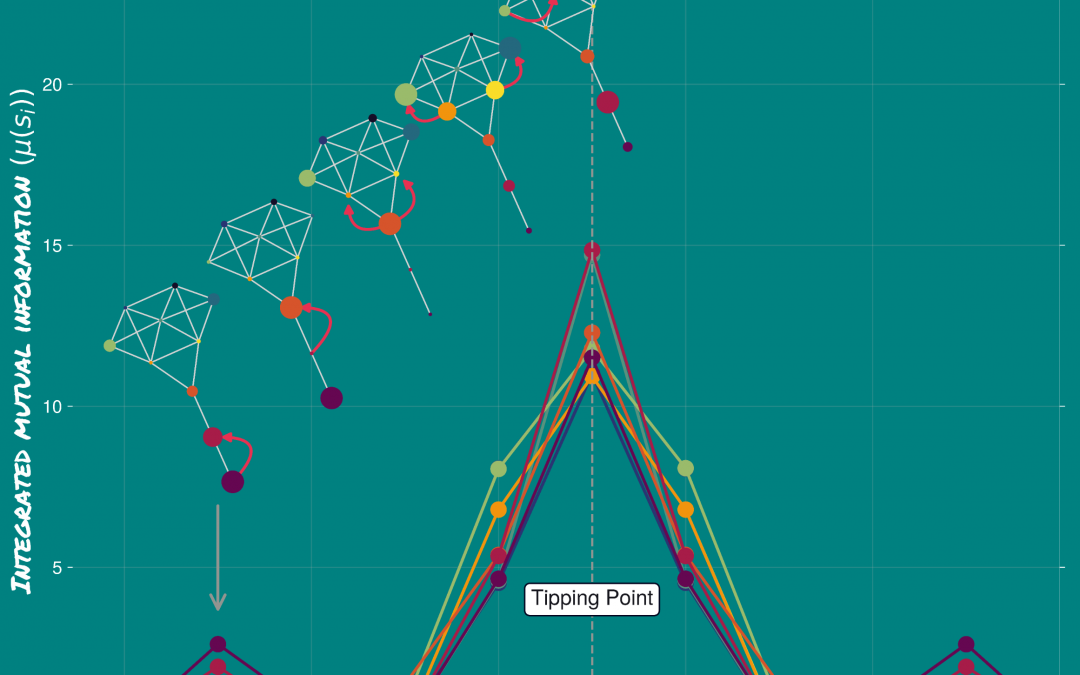
2. Domino Effect: Metastable transitions occur through a domino-like mechanism where noise propagates from low-degree to high-degree nodes. This process is driven by integrated mutual information (short-term dynamics) and asymptotic information (long-term stability).
3. Predictive Metrics: A rise in asymptotic information serves as an early warning signal for tipping points, enabling predictions about critical transitions.