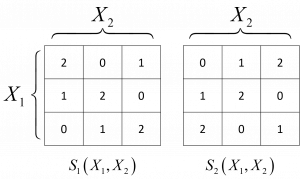
Quantifying synergy among stochastic variables is an important open problem in information theory. Information synergy occurs when multiple sources together predict an outcome variable better than the sum of single-source predictions. As simple examples, consider the correlation between one of the inputs (X1 or X2) with either output S1 or S2, which is zero, whereas taking either the inputs or the outputs together yields maximal correlation. It is an essential phenomenon in biology such as in neuronal networks and cellular regulatory processes, where different information flows integrate to produce a single response, but also in social cooperation processes as well as in statistical inference tasks in machine learning. In our publication we propose a metric of synergistic entropy and synergistic information from first principles. The proposed measure relies on so-called synergistic random variables (SRVs) which are constructed to have zero mutual information about individual source variables but non-zero mutual information about the complete set of source variables. We prove several basic and desired properties of our measure, including bounds and additivity properties. In addition, we prove several important consequences of our measure, including the fact that different types of synergistic information may co-exist between the same sets of variables. A numerical implementation is provided, which we use to demonstrate that synergy is associated with resilience to noise. Our approach is radically different from the previously proposed frameworks. Our measure may be a marked step forward in the study of multivariate information theory and its numerous applications.