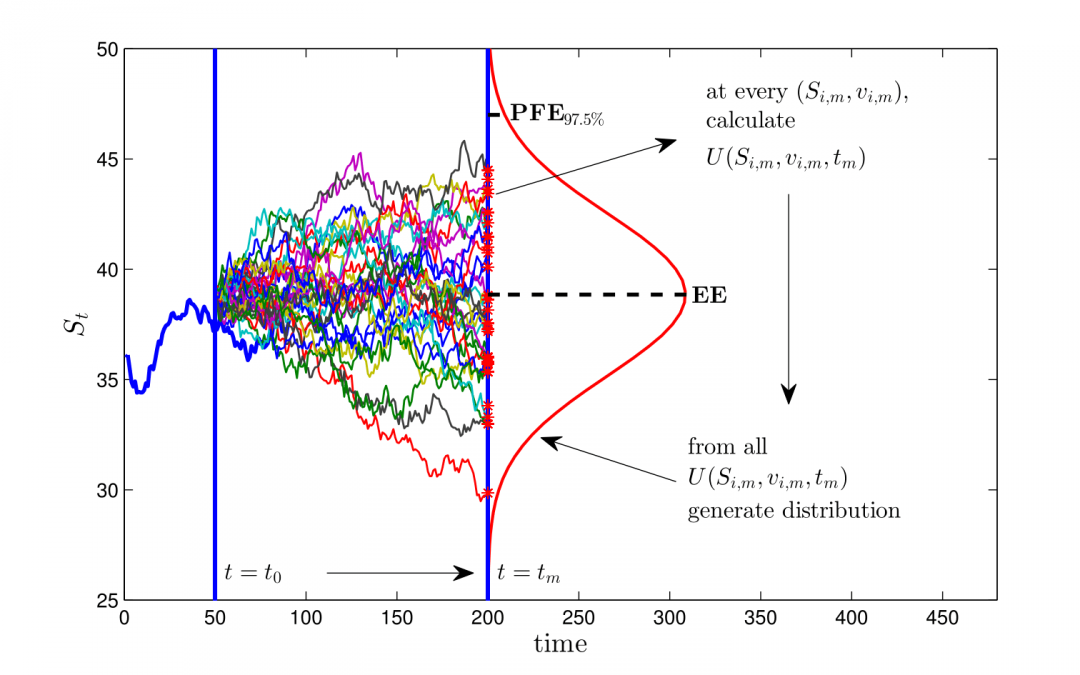
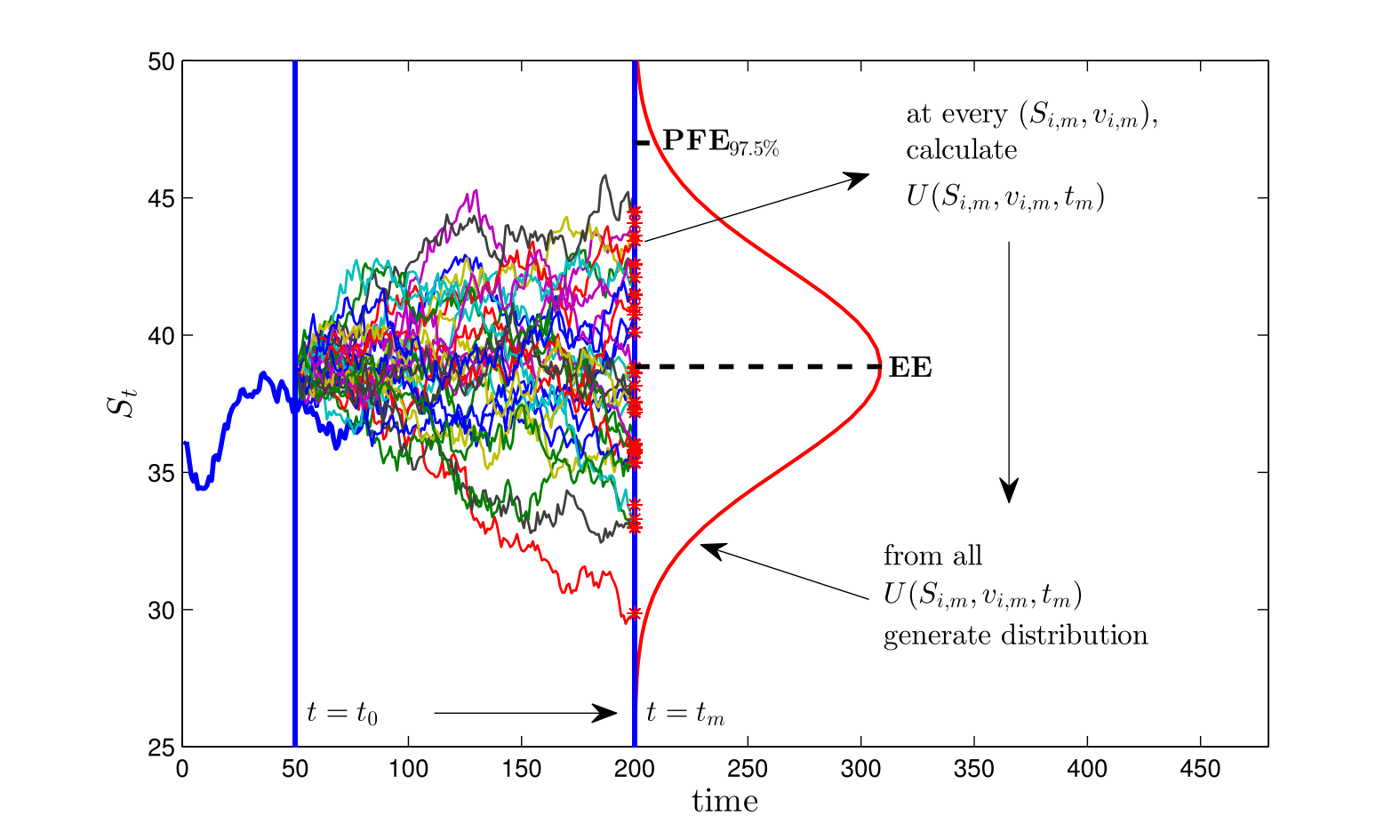
According to Basel III, financial institutions need to charge a Credit Valuation Adjustment (CVA) to account for counterparty default risk. This adjustment is typically driven by a large number of uncertain risk factors, which makes efficient computation of CVA and the corresponding risk measures a complex mathematical and numerical modelling problem.
In “Efficient Estimation of Sensitivities for Counterparty Credit Risk with the Finite Difference Monte-Carlo Method” (C.S.L. de Graaf 2016), published in the Journal of Computational Finance, Kees de Graaf, Drona Kandhai and Peter Sloot, introduced a novel and efficient numerical method for the estimation of CVA and its risk measures. For a wide range of benchmark cases, it is shown that the numerical estimates are highly accurate.
Citation info: C.S.L. de Graaf, B.D. Kandhai and P.M.A. Sloot. 2016. “Efficient estimation of sensitivities for counterparty credit risk with the finite difference Monte Carlo method.” Journal of Computational Finance 1-31.