by Mark Wijzenbroek | Dec 7, 2023 | Hot News, News
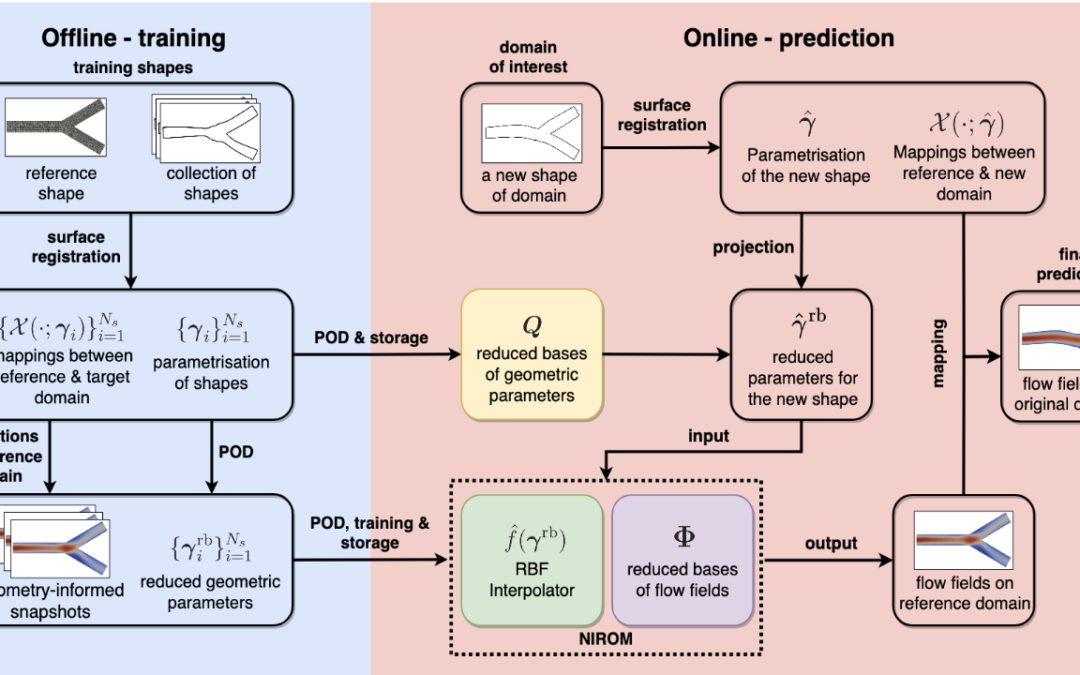
Dongwei Ye, Valeria Krzhizhanovskaya, and Alfons Hoekstra published a paper in Journal of Computational Physics on “Data-driven reduced-order modelling for blood flow simulations with geometry-informed snapshots” Parametric reduced-order modelling often...

by rob | Oct 6, 2023 | Hot News, News
The Visualisation Lab, together with researchers and therapists from Stichting Steun Emma Kinderziekenhuis, Amsterdam UMC, and Levvel have started a crowd funding campaign to help them develop a VR tool for children who are too afraid to talk. For more information and...

by Gabor Zavodszky | Jul 25, 2023 | Hot News, News
Christian Spieker, Gábor Závodszky & Alfons Hoekstra have published a new paper in Physics of Fluids that became a featured article and was published in combination with a Scilight article. When receiving a bleeding injury, the body defends itself by triggering...
by Gabor Zavodszky | Jul 25, 2023 | Hot News, News
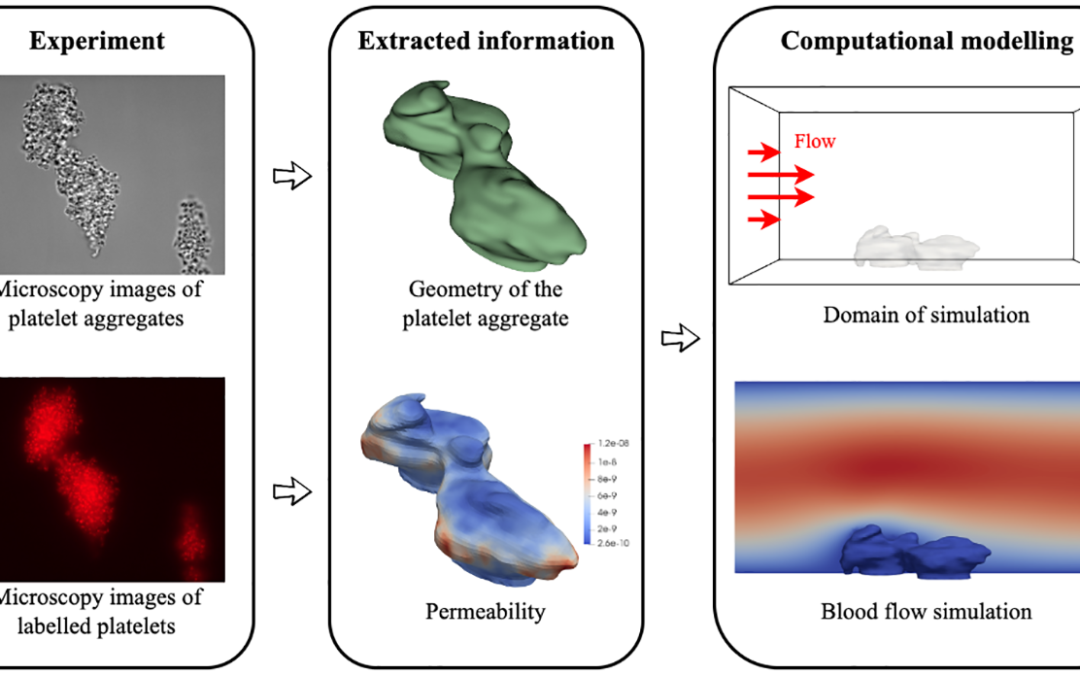
Yue Hao, Gábor Závodszky & Alfons Hoekstra have published a new paper in PLOS Computational Biology on building image based simulations of platelet aggregates. Hemodynamics is crucial for the activation and aggregation of platelets in response to flow-induced...

by Rick Quax | Jul 3, 2023 | Hot News, News
Loes Crielaard successfully defended her Ph.D. an the Agnietenkapel and was even awarded the Ph.D. ‘cum laude’. This distinction is awarded exceedingly rarely in our field. For more details, see the news...
by Vítor V. Vasconcelos | Apr 25, 2023 | Hot News, News
Dhruv Mittal and Vítor V. Vasconcelos, together with Shaul Shalvi, professor of Behavioural Ethics at the Center for Research in Experimental Economics and political Decision making (CREED), Amsterdam School of Economics, and external collaborators got their pilot...







